我們在行測備考練習的過程中經常容易忽略一個常見但又不太受重視的考點：公約數與公倍數。其實這個考點我們在小學時接觸過的，但因為年代久遠，我們有些忘記了，現在中公教育帶大家來一起回顧總結一下：

一、基本概念

1.約數、倍數：

如果一個自然數a能被自然數b整除，那么稱a為b的倍數，b為a的約數。

2.公約數、公倍數：

若一個自然數同時是若干個自然數的約數，則稱這個自然數是這若干個自然數的公約數。若一個自然數同時是若干個自然數的倍數，則稱這個自然數是這若干個自然數的公倍數。

3.最大公約數、最小公倍數：

若干個數的公約數中最大的一個就稱為這若干個自然數的最大公約數。若干個數的公倍數中最小的一個就稱為這若干個自然數的最小公倍數。

二、解題方法

(一)求最大公約數的常用方法

1.短除法

最大公約數=2×3=6

2.分解質因數法：

先分解質因數，再將相同的質因數取冪指數最小值連乘到一起

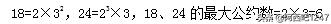
例：162和234的最大公約數為?

A.8 B.12 C.18 D.24

【答案】C

【中公解析】利用分解質因數的方法：

所以162和234的最大公約數

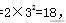
選擇C項。

求最小公倍數的常用方法

1.短除法：

注：多個數短除，要除到兩兩沒有公約數為止

2.分解質因數法：

先把這幾個數分解質因數，再將所有的質因數取冪指數最大值連乘到一起，得到的就是這幾個數的最小公倍數。

例：某三組小朋友參加趣味運動會，需要分發一千多個比賽用的小球，如果只分給A組，則A組每名小朋友可以得到25塊糖;如果只分給B組，則B組每名小朋友可以得到35塊糖;如果只分給C組，則C組每名小朋友可以得到42塊糖。那么最少再添幾個球，能使得小球平均分給三組小朋友?

A.13 B.15 C.17 D.19 【答案】C

【中公解析】根據題意，糖塊總數為25、35、42的公倍數，能滿足條件的球數只有1050個，則三組小朋友人數分別得到42人、30人、25人，共97人，1050÷97=10…80，所以還需要至少17個球，選擇C項。

三、常見應用題型

(一)周期問題

例：小陳和小李本周四于健身房相遇，已知小陳每三天去一次，小李每四天去一次，那么他們下次相遇是周幾?

周一 B.周二 C.周四 D.周五

【答案】

【中公解析】小陳每三天去一次，小李每四天去一次，周四相遇到下次相遇經過的天數需要既是3的倍數，又是4的倍數，問題為下次相遇，也就是最短相遇天數，即3和4的最小公倍數12，12÷7=1…5，所以下次相遇為周二，選擇B項。

（二）利用最大公約數求公約數的個數

例：張三有36本書，李四有48本書，現準備捐給希望工程，并平均分給幾位小朋友，有多少種不同的分法?

A.2 B.3 C.4 D.5

【答案】C

【中公解析】根據題意，所求為36和48的公約數的個數，兩者的最大公約數為6，6的約數為1、2、3、6，共四個，所以共有4種不同的分法。選擇C項。

來源：中公教育 楊蓂